如何深入理解“达西定律”

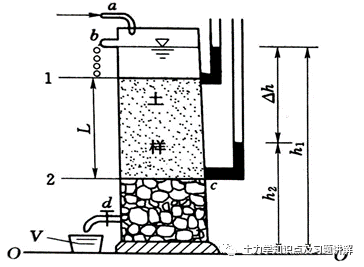
“达西定律”是描述在饱和砂土中，处于层流状态地下水的运动规律：砂土中的渗流水量_Q_与渗流的水头差(_h_1-_h_2=Δ_h_)成正比，并与通过试样的路径_L_成反比。最先是由法国科学家达西(Darcy. H)在1856年提出，采用的如下图所示的试验装置。

可用公式_v_=ki_(水力坡降_i_=Δ_h/L_，_无量纲)来表述。结合水力学中的连续性方程_Q_=_vA_，可进一步写为_Q_**= kiA，也可将达西公式写成：
**

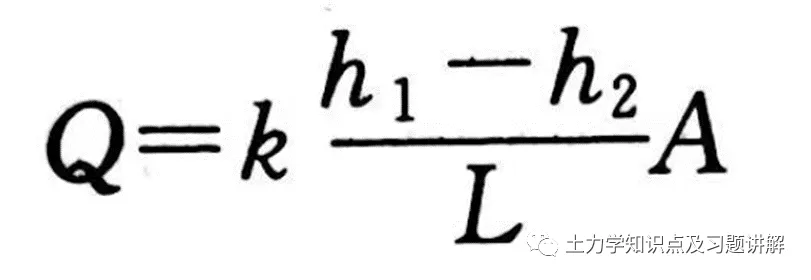
其中：_A_为垂直于渗流方向试样的截面面积；_k_为土的渗透系数。

达西定律公式较为简单，但内涵丰富，需要从以下几方面来把握：

(1)达西定律只适用饱和砂土作层流运动。因此，一般只适用于中砂、细砂、粉砂等；对于粗砂、砾石、卵石等粗颗粒会有湍流发生，不再适用。而黏性土的渗流规律不完全符合达西定律，需要修正，主要是因为黏土中自由水，需克服黏土颗粒表面结合水的粘滞阻力(即抗剪能力)才能流动，这就使得黏土发生流动要具备一定的水力坡降_i_0(即两断面需要一定大小的水头差)，即_v_=_k_(_i-i_0)。

如下图，分比为砂土(a线)、黏土(b线、近似用直线c代替)的渗透流速与坡降_i_的关系。

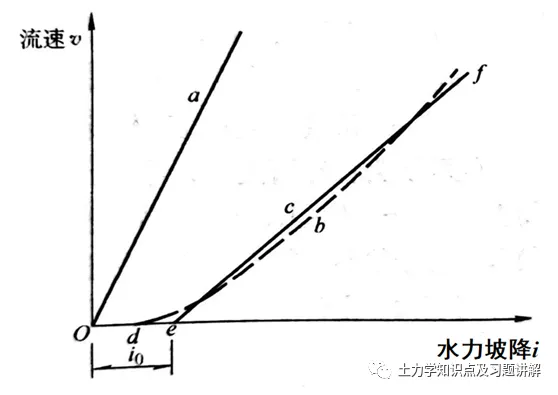
(2)水在土中渗流，依然满足水力学中的连续性方程_Q_=vA，并且孔隙中的水也不考虑其压缩性，即任何断面上的流量_Q_始终相等(若不相等，水流就不连续了，与实际不符)。渗流产生的根本原因是两断面有水头(能量)差。

(3)公式中的_v_是平均渗流速速，不是平均真实流速。这是由于水在土中的渗流不是通过土的整个截面，仅仅是通过截面内土颗粒间的孔隙，相当于实际过水断面面积比公式中的整个截面积_A_小，根据_Q_=_vA_，说明真实流速应大于公式计算得出的流速。

(4)渗透系数_k_是反映土体渗透能力强弱的一个物理量，表示单位水力坡降下土体的渗流速度，量纲与流速一致。_k_值越大，表示越容易被渗透，损失的水头(能量)就越小。其值可通过室内试验或现场试验获得，一般砂土渗透系数大于黏土。

(5) 渗透系数_k_的大小与土的密实度(孔隙比)成反比；与土颗粒尺寸、土的饱和度、水温成正比，级配越好的土(因为不均匀系数越大)，_k_越小。此外，还与土的结构和矿物组成有关。

注意：“根据公式_v_=ki，当渗透流速一定_v_时，水力坡降_i_与渗透系数_k_成反比。”这种说法是错误的，因为_k_可理解土的一种固有属性，与外界的坡降和流速是无关的，可类比于：质量=密度×体积，不能说质量一定，体积越大，密度越小，因为密度是物体的固有属性。

(6)针对于多层土的计算，依然可以采取达西公式_v_=k__Δ__h/L_或_Q= _kiA_。只不过，计算得到的_k_为多层土的平均渗透系数或成等效渗透系数，_i_为多层土的平均渗流坡降，_L_仍为初断面(流进断面)与末断面的渗流距离。